Cada vez más, los gerentes e ingenieros responsables de la fabricación y otras actividades industriales están incorporando un enfoque de confiabilidad en sus planes e iniciativas estratégicas y tácticas. Esta tendencia está afectando numerosas áreas funcionales, incluido el diseño y adquisición de máquinas / sistemas, las operaciones de la planta y el mantenimiento de la planta.
Con sus orígenes en la industria de la aviación, la ingeniería de confiabilidad, como disciplina, se ha centrado históricamente principalmente en garantizar la confiabilidad del producto. Cada vez más, estos métodos se están empleando para garantizar la fiabilidad de la producción de las plantas y equipos de fabricación, a menudo como un facilitador para la manufactura esbelta. Este artículo proporciona una introducción a los métodos más relevantes y prácticos para la ingeniería de confiabilidad de la planta, que incluyen:
- Cálculos básicos de confiabilidad para tasa de falla, MTBF, disponibilidad, etc.
- Una introducción a la distribución exponencial: la piedra angular de los métodos de confiabilidad.
- Identificar dependencias de tiempo de falla utilizando el versátil sistema Weibull.
- Desarrollar un sistema efectivo de recolección de datos de campo.
Historia de Ingeniería de Confiabilidad
Los orígenes del campo de la ingeniería de confiabilidad, se remontan al punto en que el hombre comenzó a depender de las máquinas para su subsistencia. La Noria, por ejemplo, es una bomba antigua que se cree que es la primera máquina so sticada del mundo. Utilizando la energía hidráulica del flujo de un río o arroyo, las personas utilizaron cubos para transferir agua a los canales, viaductos y otros dispositivos de distribución para regar los campos y proporcionar agua a las comunidades.
Si la Noria fracasaba, las personas que dependían de ella para su suministro de alimentos estaban en riesgo. La supervivencia siempre ha sido una gran fuente de motivación para la confiabilidad.
Si bien los orígenes de su demanda son antiguos, la ingeniería de confiabilidad como disciplina técnica realmente floreció junto con el crecimiento de la aviación comercial después de la Segunda Guerra Mundial. Rápidamente se hizo evidente para los gerentes de las compañías de la industria de la aviación que los accidentes eran malos para sus negocios. Karen Bernowski, editora de Quality Progress , reveló en una de sus editoriales una investigación sobre el valor mediático de la muerte por diversos medios, realizada por el profesor de estadística del MIT Arnold Barnett e informada en 1994.
Barnett evaluó el número de artículos de primera plana del New York Times por cada 1,000 muertes por diversos medios. ¡Encontró que las muertes relacionadas con el cáncer arrojaron 0.02 artículos de primera plana por cada 1,000 muertes, el homicidio arrojó 1.7 por 1,000 muertes, el SIDA arrojó 2.3 por 1,000 muertes, y los accidentes relacionados con la aviación arrojaron 138.2 artículos por 1,000 muertes!
El costo y la naturaleza de alto per l de los accidentes relacionados con la aviación ayudaron a motivar a la industria de la aviación a participar en gran medida en el desarrollo de la disciplina de ingeniería de confiabilidad. Del mismo modo, debido a la naturaleza crítica del equipo militar en defensa, las técnicas de ingeniería de confiabilidad se han empleado durante mucho tiempo para asegurar la preparación operativa. Muchos de nuestros estándares en el campo de la ingeniería de confiabilidad son estándares MIL o tienen su origen en actividades militares.
¿Qué es la ingeniería de confiabilidad?
La ingeniería de confiabilidad se ocupa de la longevidad y confiabilidad de las piezas, productos y sistemas. Más conmovedor, se trata de controlar el riesgo. La ingeniería de confiabilidad incorpora una amplia variedad de técnicas analíticas diseñadas para ayudar a los ingenieros a comprender los modos y patrones de falla de estas piezas, productos y sistemas. Tradicionalmente, el campo de la ingeniería de confiabilidad se ha centrado en la fiabilidad del producto y la garantía de fiabilidad.
En los últimos años, las organizaciones que implementan máquinas y otros activos físicos en entornos de producción han comenzado a implementar varios principios de ingeniería de confiabilidad con el propósito de garantizar la confiabilidad y la confiabilidad de la producción.
Cada vez más, las organizaciones de producción implementan técnicas de ingeniería de confiabilidad como el Mantenimiento Centrado en la Confiabilidad (RCM), que incluye modos de falla y análisis de efectos (y criticidad) (FMEA, FMECA), análisis de causa raíz (RCA) , mantenimiento basado en condiciones, esquemas de planificación de trabajo mejorados. Estas mismas organizaciones están comenzando a adoptar estrategias de diseño y adquisición basadas en el costo del ciclo de vida, esquemas de gestión de cambios y otras herramientas y técnicas avanzadas para controlar las causas fundamentales de la baja confiabilidad.
Sin embargo, la adopción de los aspectos más cuantitativos de la ingeniería de confiabilidad por parte de la comunidad de confiabilidad ha sido lenta. Esto se debe en parte a la complejidad percibida de las técnicas y en parte a la dificultad para obtener datos útiles.
Los aspectos cuantitativos de la ingeniería de confiabilidad pueden parecer, en la superficie, complicados y desalentadores. En realidad, sin embargo, una comprensión relativamente básica de los métodos más fundamentales y ampliamente aplicables puede permitir al ingeniero de confiabilidad de la planta obtener una comprensión mucho más clara sobre dónde están ocurriendo los problemas, su naturaleza y su impacto en el proceso de producción, al menos en lo cuantitativo sentido.
Utilizados adecuadamente, las herramientas y métodos de ingeniería de confiabilidad cuantitativa permiten que la ingeniería de con abilidad de la planta aplique de manera más efectiva los marcos proporcionados por RCM, RCA, etc., eliminando algunas de las conjeturas relacionadas con su aplicación. Sin embargo, los ingenieros deben ser particularmente inteligentes en su aplicación de los métodos.
¿Por qué? El contexto operativo y el entorno de un proceso de producción incorpora más variables que el mundo unidimensional de la garantía de fiabilidad del producto. Esto se debe a la influencia combinada de la ingeniería de diseño, adquisición, producción, operaciones, mantenimiento, etc., y la dificultad de crear pruebas y experimentos efectivos para modelar los aspectos multidimensionales de un entorno de producción típico.
A pesar de la mayor dificultad en la aplicación de métodos de confiabilidad cuantitativa en el entorno de producción, vale la pena obtener una buena comprensión de las herramientas y aplicarlas cuando sea apropiado. Los datos cuantitativos ayudan a de nir la naturaleza y la magnitud de un problema u oportunidad, lo que proporciona una visión de la con fiabilidad en su aplicación de otras herramientas de ingeniería de confiabilidad.
Este artículo proporcionará una introducción a los métodos de ingeniería de confiabilidad más básicos que son aplicables al ingeniero de planta interesado en el aseguramiento de la confiabilidad de la producción. Presupone una comprensión básica del álgebra, la teoría de la probabilidad y las estadísticas univariadas basadas en la distribución gaussiana (normal) (por ejemplo, medida de tendencia central, medidas de dispersión y variabilidad, intervalos de confianza, etc.).
Debe quedar claro que este documento es una breve introducción a los métodos de confiabilidad. De ninguna manera es una encuesta exhaustiva de los métodos de ingeniería de confiabilidad, ni de ninguna manera es nueva o no convencional. Los métodos descritos en este documento son utilizados habitualmente por ingenieros de confiabilidad y son conceptos básicos de conocimiento para aquellos que buscan la certificación profesional de la Sociedad Americana de Calidad (ASQ) como ingeniero de con abilidad (CRE).
En la bibliografía de este artículo se enumeran varios libros sobre ingeniería de confiabilidad. El autor de este artículo ha encontrado que los Métodos de confiabilidad para ingenieros de KS Krishnamoorthi y las Estadísticas de confiabilidad de Robert Dovich son referencias particularmente útiles y fáciles de usar sobre el tema de los métodos de ingeniería de con abilidad. Ambos son publicados por ASQ Press. Antes de analizar los métodos, debe familiarizarse con la nomenclatura de ingeniería de confiabilidad. Para mayor comodidad, en el apéndice de este artículo se proporciona una lista muy resumida de términos y definiciones clave. Para obtener una definición más exhaustiva de los términos y la nomenclatura de confiabilidad, consulte MIL-STD-721 y otras normas relacionadas. Las definiciones contenidas en el apéndice son de MIL-STD-721.
Conceptos matemáticos básicos en ingeniería de confiabilidad
Muchos conceptos matemáticos se aplican a la ingeniería de confiabilidad, particularmente desde las áreas de probabilidad y estadística. Del mismo modo, muchas distribuciones matemáticas pueden utilizarse para diversos fines, incluida la distribución gaussiana (normal), la distribución log-normal, la distribución de Rayleigh, la distribución exponencial, la distribución de Weibull y una gran cantidad de otras.
Para el propósito de esta breve introducción, limitaremos nuestra discusión a la distribución exponencial y la distribución de Weibull, las dos más ampliamente aplicadas a la ingeniería de confiabilidad. En aras de la brevedad y la simplicidad, se han excluido conceptos matemáticos importantes como la distribución de la bondad de ajuste y los intervalos de confianza.
Tasa de falla y tiempo medio entre / hasta la falla (MTBF / MTTF)
El propósito de las mediciones cuantitativas de confiabilidad es definir la tasa de falla en relación con el tiempo y modelar esa tasa de falla en una distribución matemática con el propósito de comprender los aspectos cuantitativos de la falla. El bloque de construcción más básico es la tasa de falla, que se estima utilizando la siguiente ecuación:
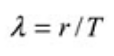
Donde:
λ = Tasa de falla (a veces denominada tasa de riesgo)
T = Tiempo total de funcionamiento / ciclos / millas / etc. durante un período de investigación para artículos fallidos y no fallidos.
r = El número total de fallas que ocurren durante el período de investigación.
Por ejemplo, si cinco motores eléctricos funcionan durante un tiempo total colectivo de 50 años con cinco fallas funcionales durante el período, la tasa de falla es de 0.1 fallas por año.
Otro concepto muy básico es el tiempo medio entre / hasta la falla (MTBF / MTTF). La única diferencia entre MTBF y MTTF es que empleamos MTBF cuando nos referimos a artículos que se reparan cuando fallan. Para los artículos que simplemente se tiran y se reemplazan, utilizamos el término MTTF. Los cálculos son iguales.
El cálculo básico para estimar el tiempo medio entre fallas (MTBF) y el tiempo medio hasta fallas (MTTF), ambas medidas de tendencia central, es simplemente el recíproco de la función de tasa de fallas. Se calcula usando la siguiente ecuación.
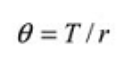
Donde:
θ = Tiempo medio entre / hasta la falla
T = Tiempo total de funcionamiento / ciclos / millas / etc. durante un período de investigación para artículos fallidos y no fallidos.
r = El número total de fallas que ocurren durante el período de investigación.
El MTBF para nuestro ejemplo de motor eléctrico industrial es de 10 años, que es el recíproco de la tasa de falla de los motores. Por cierto, estimaríamos MTBF para motores eléctricos que se reconstruyen en caso de falla. Para motores más pequeños que se consideran desechables, declararíamos la medida de tendencia central como MTTF.
La tasa de falla es un componente básico de muchos cálculos de con abilidad más complejos. Dependiendo del diseño mecánico / eléctrico, el contexto operativo, el entorno y / o la efectividad del mantenimiento, la tasa de falla de una máquina en función del tiempo puede disminuir, permanecer constante, aumentar linealmente o aumentar geométricamente (Figura 1). La importancia de la tasa de falla frente al tiempo se discutirá con más detalle más adelante.
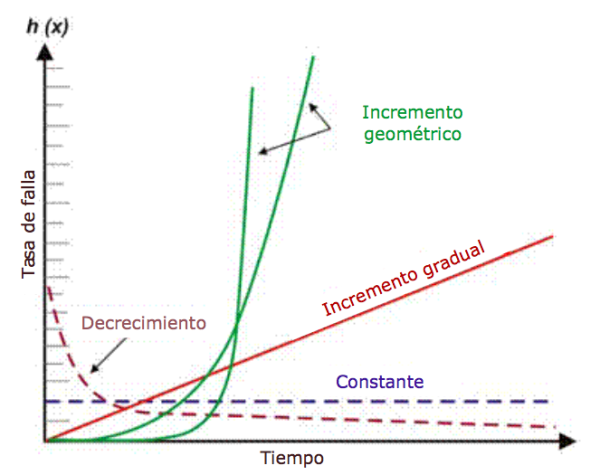
Figura 1. Diferentes tasas de falla versus escenarios de tiempo
La curva de la ‘bañera’
Las personas que han recibido solo capacitación básica en probabilidad y estadística probablemente estén más familiarizadas con la distribución gaussiana o normal, que está asociada con la curva de densidad de probabilidad en forma de campana. La distribución gaussiana es generalmente aplicable a los conjuntos de datos donde las dos medidas más comunes de tendencia central, media y mediana, son aproximadamente iguales.
Sorprendentemente, a pesar de la versatilidad de la distribución gaussiana en el modelado de probabilidades para fenómenos que van desde puntajes de pruebas estandarizadas hasta el peso al nacer de los bebés, no es la distribución dominante empleada en ingeniería de confiabilidad. La distribución gaussiana tiene su lugar en la evaluación de las características de falla de las máquinas con un modo de falla dominante, pero la distribución primaria empleada en la ingeniería de confiabilidad es la distribución exponencial.
Al evaluar la confiabilidad y las características de falla de una máquina, debemos comenzar con la curva muy difamada de la “bañera”, que refleja la tasa de falla en función del tiempo (Figura 2). En concepto, la curva de la bañera demuestra efectivamente las tres características básicas de la tasa de falla de una máquina: en declive, constante o creciente. Lamentablemente, la curva de la bañera ha sido duramente criticada en la literatura de ingeniería de mantenimiento porque no logra modelar de manera efectiva la tasa de falla característica para la mayoría de las máquinas en una planta industrial, lo que generalmente es cierto a nivel macro.
La mayoría de las máquinas pasan sus vidas en la vida temprana, o mortalidad infantil, y / o las regiones de tasa de falla constante de la curva de la bañera. Raramente vemos fallas sistémicas basadas en el tiempo en máquinas industriales. A pesar de sus limitaciones para modelar las tasas de falla de las máquinas industriales típicas, la curva de la bañera es una herramienta útil para explicar los conceptos básicos de la ingeniería de confiabilidad.
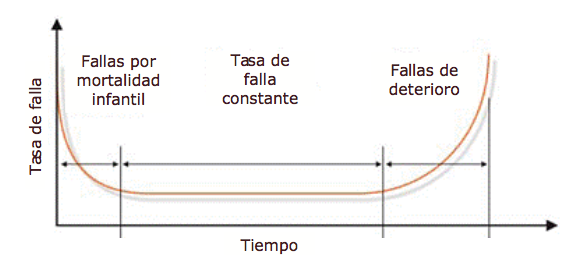
Figura 2. La curva de ‘bañera’ muy difamada
El cuerpo humano es un excelente ejemplo de un sistema que sigue la curva de la bañera. Las personas, y otras especies orgánicas, tienden a sufrir una alta tasa de fracaso (mortalidad) durante sus primeros años de vida, particularmente los primeros años, pero la tasa disminuye a medida que el niño crece. Suponiendo que una persona alcanza la pubertad y sobrevive a su adolescencia, su tasa de mortalidad se vuelve bastante constante y permanece allí hasta que las enfermedades dependientes de la edad (tiempo) comienzan a aumentar la tasa de mortalidad (desgaste).
Numerosas influencias afectan las tasas de mortalidad, incluida la atención prenatal y la nutrición de la madre, la calidad y disponibilidad de la atención médica, el medio ambiente y la nutrición, las opciones de estilo de vida y, por supuesto, la predisposición genética. Estos factores pueden compararse metafóricamente con factores que influyen en la vida útil de la máquina. El diseño y la adquisición son análogos a la predisposición genética; la instalación y puesta en servicio es análoga a la atención prenatal y la nutrición de la madre; y las opciones de estilo de vida y la disponibilidad de atención médica es análoga a la efectividad del mantenimiento y al control proactivo sobre las condiciones operativas.
La distribución exponencial
La distribución exponencial, la fórmula de predicción de confiabilidad más básica y ampliamente utilizada, modela máquinas con la tasa de falla constante o la sección plana de la curva de la bañera. La mayoría de las máquinas industriales pasan la mayor parte de sus vidas en la tasa de falla constante, por lo que es ampliamente aplicable. A continuación se muestra la ecuación básica para estimar la confiabilidad de una máquina que sigue la distribución exponencial, donde la tasa de falla es constante en función del tiempo.
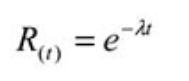
Donde:
R (t) = Estimación de confiabilidad para un período de tiempo, ciclos, millas, etc. (t). e = Base de los logaritmos naturales (2.718281828)
λ = Tasa de falla (1 / MTBF o 1 / MTTF)
En nuestro ejemplo de motor eléctrico, si supone una tasa de falla constante, la probabilidad de operar un motor durante seis años sin una falla, o la confiabilidad proyectada, es del 55 por ciento. Esto se calcula de la siguiente manera:
R (6) = 2.718281828- (0.1 * 6) R (6) = 0.5488 = ~ 55%
En otras palabras, después de seis años, se puede esperar que cerca del 45% de la población de motores idénticos que operan en una aplicación idéntica fallen. Vale la pena reiterar en este punto que estos cálculos proyectan la probabilidad para una población. Cualquier individuo de la población podría fallar el primer día de operación, mientras que otro individuo podría durar 30 años. Esa es la naturaleza de las proyecciones de confiabilidad probabilística.
Una característica de la distribución exponencial es que el MTBF se produce en el punto en el que la fiabilidad calculada es del 36,78%, o el punto en el que el 63,22% de las máquinas ya han fallado. En nuestro ejemplo de motor, después de 10 años, se puede esperar que el 63.22% de los motores de una población de motores idénticos que sirven en aplicaciones idénticas fallen. En otras palabras, la tasa de supervivencia es del 36,78% de la población.
A menudo hablamos de la vida proyectada del rodamiento como la vida L10. Este es el momento en el que se espera que falle el 10% de una población de rodamientos (tasa de supervivencia del 90%). En realidad, solo una fracción de los rodamientos sobrevive hasta el punto L10. Hemos llegado a aceptar eso como la vida objetiva de un rodamiento cuando quizás deberíamos poner nuestra mira en el punto L63.22, lo que indica que nuestros rodamientos duran, en promedio, el MTBF proyectado, suponiendo, por supuesto, que los rodamientos sigue la distribución exponencial. Discutiremos ese tema más adelante en la sección de análisis de Weibull del artículo.
La función de densidad de probabilidad (pdf), o distribución de vida, es una ecuación matemática que se aproxima a la distribución de frecuencia de falla. Es el pdf, o distribución de frecuencia de vida, el que produce la curva familiar en forma de campana en la distribución gaussiana o normal. A continuación se muestra el pdf para la distribución exponencial.
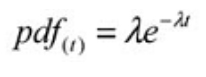
Donde:
pdf (t) = Distribución de frecuencia de vida para un tiempo dado (t) e = Base de los logaritmos naturales (2.718281828)
λ = Tasa de falla (1 / MTBF o 1 / MTTF)
En nuestro ejemplo de motor eléctrico, la probabilidad real de falla a los tres años se calcula de la siguiente manera:
pdf (3) = 0.1 * 2.718281828- (0.1 * 3)
pdf (3) = 0.1 * 0.7408
pdf (3) = .07408 = ~ 7.4%
En nuestro ejemplo, si asumimos una tasa de falla constante, que sigue la distribución exponencial, la distribución de vida útil o pdf para los motores eléctricos industriales, se expresa en la Figura 3. No se confunda con la naturaleza decreciente de la función pdf. Sí, la tasa de fallas es constante, pero el pdf matemáticamente asume fallas sin reemplazo, por lo que la población a partir de la cual pueden ocurrir fallas se reduce continuamente, acercándose asintóticamente a cero.
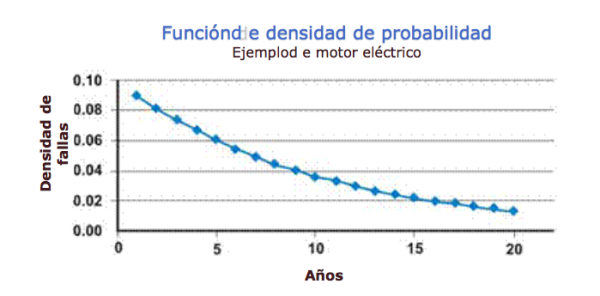
Figura 3. La función de densidad de probabilidad (pdf)
La función de distribución acumulativa (cdf) es simplemente el número acumulado de fallas que uno podría esperar durante un período de tiempo. Para la distribución exponencial, la tasa de falla es constante, por lo que la tasa relativa a la cual los componentes fallados se agregan al cdf permanece constante. Sin embargo, a medida que la población disminuye como resultado del fracaso, el número real de fallas estimadas matemáticamente disminuye en función de la población en declive. Al igual que el pdf se acerca asintóticamente a cero, el cdf se acerca asintóticamente a uno (Figura 4).
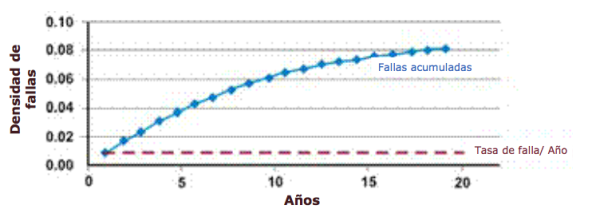
Figura 4. Tasa de falla y la función de distribución acumulativa
La parte de la tasa de fracaso decreciente de la curva de la bañera, que a menudo se denomina región de mortalidad infantil, y la región de desgaste se discutirán en la siguiente sección que trata la distribución versátil de Weibull.
Distribución Weibull
Originalmente desarrollado por Wallodi Weibull, un matemático sueco, el análisis de Weibull es fácilmente la distribución más versátil empleada por los ingenieros de confiabilidad. Si bien se llama distribución, en realidad es una herramienta que permite al ingeniero de confiabilidad caracterizar primero la función de densidad de probabilidad (distribución de frecuencia de falla) de un conjunto de datos de falla para caracterizar las fallas como vida temprana, constante (exponencial) o desgaste (Gaussiano o log normal) al graficar los datos de tiempo hasta la falla en un papel de trazado especial con el registro de los tiempos / ciclos / millas a la falla trazó un eje X escalado de registro frente al porcentaje acumulado de la población representada por cada falla en un registro -log eje Y escalado (Figura 5).
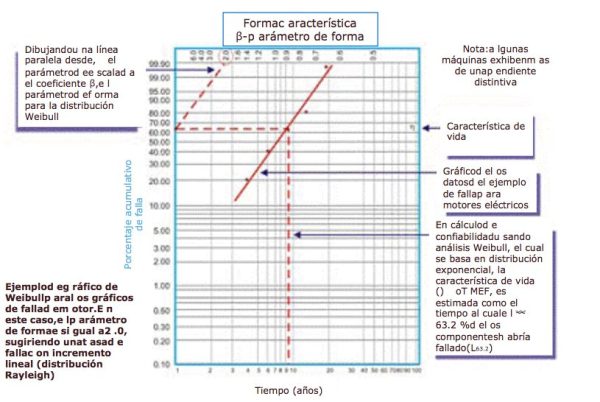
Figura 5. La trama simple de Weibull
Una vez trazada, la pendiente lineal de la curva resultante es una variable importante, llamada parámetro de forma, representada por â, que se utiliza para ajustar la distribución exponencial para que se ajuste a un gran número de distribuciones de fallas. En general, si el coeficiente â, o parámetro de forma, es menor que 1.0, la distribución exhibe fallas en la vida temprana o mortalidad infantil. Si el parámetro de forma excede aproximadamente 3.5, los datos dependen del tiempo e indican fallas de desgaste.
Este conjunto de datos generalmente asume la distribución gaussiana o normal. A medida que el coeficiente â aumenta por encima de ~ 3.5, la distribución en forma de campana se tensa, exhibiendo una curtosis creciente (pico en la parte superior de la curva) y una desviación estándar más pequeña. Muchos conjuntos de datos exhibirán dos o incluso tres regiones distintas.
Es común que los ingenieros de con abilidad tracen, por ejemplo, una curva que representa el parámetro de forma durante la ejecución y otra curva para representar la tasa de falla constante o gradualmente creciente. En algunos casos, emerge una tercera pendiente lineal distinta para identificar una tercera forma, la región de desgaste.
En estos casos, el pdf de los datos de falla asume, de hecho, la forma familiar de la curva de la bañera (Figura 6). Sin embargo, la mayoría de los equipos mecánicos utilizados en las plantas exhiben una región de mortalidad infantil y una región de tasa de falla constante o gradualmente creciente. Es raro ver emerger una curva que representa el desgaste. La vida característica, o η (minúscula griega “Eta”), es la aproximación Weibull del MTBF. Siempre es función del tiempo, millas o ciclos donde el 63.21% de las unidades bajo evaluación han fallado, que es el MTBF / MTTF para la distribución exponencial.
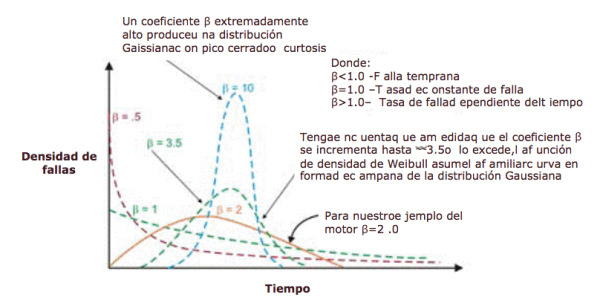
Figura 6. Dependiendo del parámetro de forma, la curva de densidad de falla de Weibull puede asumir varias distribuciones, que es lo que la hace tan versátil para la ingeniería de confiabilidad.
Como advertencia para vincular esta herramienta a la excelencia en el mantenimiento y la excelencia de las operaciones, si tuviéramos que controlar de manera más efectiva las funciones de forzamiento que conducen a fallas mecánicas en los cojinetes, engranajes, etc., tales como lubricación, control de contaminación, alineación, equilibrio, operación apropiada, etc., más máquinas realmente alcanzarían su vida de fatiga. Las máquinas que alcanzan su vida de fatiga exhibirán la característica de desgaste familiar.
El uso del coeficiente β para ajustar la ecuación de la tasa de falla en función del tiempo arroja la siguiente ecuación general:
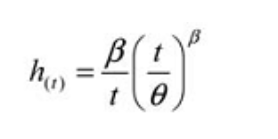
Donde:
h (t) = tasa de falla (o tasa de riesgo) para un tiempo dado (t) e = Base de los logaritmos naturales (2.718281828)
θ = MTBF / MTTF
β estimado = Parámetro de forma de Weibull del grá co.
Y, la siguiente función de con abilidad:
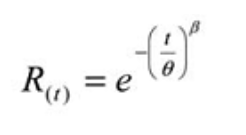
Donde:
R (t) = Estimación de con abilidad para un período de tiempo, ciclos, millas, etc. (t) e = Base de los logaritmos naturales (2.718281828)
θ = MTBF / MTTF
β estimado = Weibull parámetro de forma de la trama.
Y, la siguiente función de densidad de probabilidad (pdf):
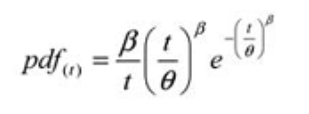
Donde:
pdf (t) = Estimación de la función de densidad de probabilidad para un período de tiempo, ciclos, millas, etc. (t)
e = Base de los logaritmos naturales (2.718281828)
θ = Estimado MTBF / MTTF
β = Parámetro de forma de Weibull del grá co.
Cabe señalar que cuando β es igual a 1.0, la distribución de Weibull toma la forma de la distribución exponencial en la que se basa.
Para los no iniciados, las matemáticas requeridas para realizar el análisis de Weibull pueden parecer desalentadoras. Pero una vez que entiendes la mecánica de las fórmulas, las matemáticas son realmente bastante simples. Además, el software hará la mayor parte del trabajo por nosotros hoy, pero es importante tener una comprensión de la teoría subyacente para que el ingeniero de confiabilidad de la planta pueda implementar efectivamente la poderosa técnica de análisis de Weibull.
En nuestro ejemplo anteriormente discutido de motores eléctricos, asumimos previamente la distribución exponencial. Sin embargo, si el análisis de Weibull revelara fallas en la vida temprana al producir un parámetro de forma β de 0.5, la estimación de confiabilidad a los seis años sería ~ 46%, no el ~ 55% estimado asumiendo la distribución exponencial. Para reducir las fallas de desgaste, necesitaríamos confiar en nuestros proveedores para proporcionar una calidad y confiabilidad mejor construidas y entregadas, almacenar los motores mejor para evitar el óxido, la corrosión, el desgaste y otros mecanismos de desgaste estático, y hacer un mejor trabajo de instalación y puesta en marcha de máquinas nuevas o reconstruidas.
Por el contrario, si el análisis de Weibull reveló que los motores exhibieron fallas predominantemente relacionadas con el desgaste, produciendo un parámetro de forma β de 5.0, la estimación de confiabilidad a los seis años sería ~ 93%, en lugar del ~ 55% estimado asumiendo la distribución exponencial. Para fallas de desgaste dependientes del tiempo, podemos realizar revisiones o reemplazos programados, suponiendo que tengamos una buena estimación del MTBF / MTTF después de haber alcanzado la región de desgaste y una desviación estándar lo suficientemente pequeña como para tomar decisiones de reconstrucción o reemplazo de alta confianza que no son muy costosos.
En nuestro ejemplo del motor, suponiendo un parámetro de forma β de 5.0, la tasa de falla comienza a aumentar rápidamente después de unos cinco o seis años, por lo que es posible que deseemos editar nuestros datos para centrarnos solo en la región de desgaste al estimar el reemplazo o la reconstrucción basada en el tiempo hora. Alternativamente, podemos mejorar el diseño, apuntando a los modos de falla dominantes con el objetivo de disminuir las interferencias de “resistencia al estrés”. En otras palabras, podemos intentar eliminar las debilidades de la máquina mediante la modificación del diseño, con el objetivo de eliminar lo que sea que esté causando las fallas dependientes del tiempo.
Suponiendo que todo es constante, excepto el parámetro de forma β, la Figura 7 ilustra la diferencia que tiene el parámetro de forma β en la estimación de confiabilidad asumiendo valores de forma β de 0.5 (vida temprana), 1.0 (constante o exponencial) y 5.0 (desgaste) para un rango de estimaciones de tiempo. Este gráfico ilustra visualmente el concepto de aumentar el riesgo frente al tiempo (β = 0.5), el riesgo constante frente al tiempo (β = 1.0) y el aumento del riesgo frente al tiempo (β = 5).
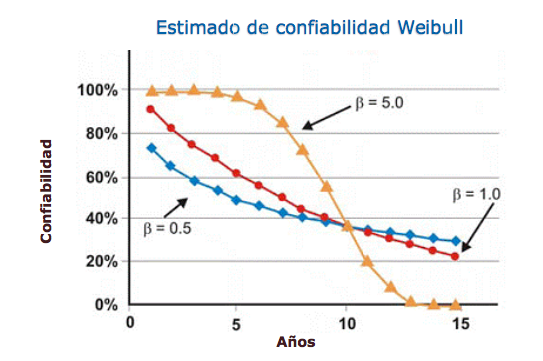
Figura 7. Diversas proyecciones de confiabilidad en función del tiempo para diferentes parámetros de forma de Weibull
La trama de Weibull de múltiples pendientes
Con frecuencia, cuando se dibuja una línea de regresión de mejor ajuste a través de los puntos de datos en un gráfico de Weibull, el coeficiente de correlación es pobre, lo que significa que los puntos de datos reales se desvían una gran distancia de la línea de regresión. Esto se evalúa examinando el coeficiente de correlación R, o más conservadoramente, R2, que denota la variabilidad de los datos. Cuando la correlación es pobre, el ingeniero de confiabilidad debe examinar los datos para evaluar si existen dos o más patrones, lo que puede denotar diferencias importantes en los modos de falla, contexto operativo, etc. A menudo, esto produce dos o más estimaciones de beta (Figura 8).
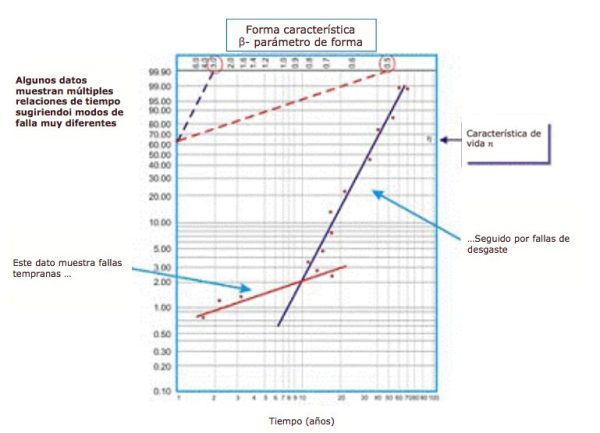
Figura 8. Un ejemplo de un diagrama de Weibull Multi-beta
Como vemos en nuestro ejemplo en la Figura 8, el conjunto de datos funciona mejor cuando se dibujan dos líneas de regresión distintas. La primera línea, exhibe un parámetro de forma beta de 0.5, lo que sugiere fallas en la vida temprana. La segunda línea exhibe una forma beta de 3.0, lo que sugiere que el riesgo de falla aumenta en función del tiempo. Es común que los equipos complejos, en particular los equipos mecánicos, experimenten fallas de “arranque” cuando se reconstruyen nuevos o recientemente. Como tal, el riesgo de falla es mayor solo después del arranque inicial.
Una vez que el sistema funciona durante su período de ejecución, que puede llevar minutos, horas, días, semanas, meses o años, dependiendo del tipo de sistema, el sistema entra en un patrón de riesgo diferente. En este ejemplo, el sistema ingresa en un período en el que el riesgo de falla aumenta en función del tiempo una vez que el sistema sale de su período inicial.
El multi-beta ofrece al ingeniero de confiabilidad una estimación más precisa del riesgo en función del tiempo. Armado con este conocimiento, él o ella están mejor posicionados para tomar medidas atenuantes. Por ejemplo, durante el período de vida temprana, estaríamos inclinados a mejorar la precisión con la que fabricamos / reconstruimos, instalamos y ponemos en marcha. Además, podríamos agregar técnicas de monitoreo y / o aumentar nuestra frecuencia de monitoreo durante el período de alto riesgo. Después del período de rodaje, podríamos introducir técnicas de monitoreo dirigidas a las fallas de desgaste dependientes del tiempo que se cree que afectan el sistema, aumentar la frecuencia de monitoreo en consecuencia o programar acciones de mantenimiento preventivo “difíciles” en algunos casos.
Estimación de la confiabilidad del sistema
Una vez que se ha establecido la confiabilidad de los componentes o las máquinas en relación con el contexto operativo y el tiempo de misión requerido, los ingenieros de la planta deben evaluar la confiabilidad de un sistema o proceso. Nuevamente, en aras de la brevedad y la simplicidad, discutiremos las estimaciones de confiabilidad del sistema para sistemas redundantes de carga compartida, serie y paralelo (sistemas r / n).
Sistemas en serie
Antes de analizar los sistemas en serie, deberíamos analizar los diagramas de bloques de confiabilidad. No es una herramienta complicada de usar, los diagramas de bloques de confiabilidad simplemente mapean un proceso de principio a n. Para un sistema en serie, el subsistema A es seguido por el subsistema B y así sucesivamente. En el sistema en serie, la capacidad de emplear el subsistema B depende del estado operativo del subsistema A. Si el subsistema A no está funcionando, el sistema está inactivo independientemente de la condición del subsistema B (Figura 9).
Para calcular la confiabilidad del sistema para un proceso en serie, solo necesita multiplicar la confiabilidad estimada del Subsistema A en el tiempo (t) por la confiabilidad estimada del Subsistema B en el tiempo (t). La ecuación básica para calcular la confiabilidad del sistema de un sistema de serie simple es:

Donde:
Rs (t) – Fiabilidad del sistema para un tiempo dado (t)
R1-n (t) – Fiabilidad del subsistema o subfunción para un tiempo dado (t)
Entonces, para un sistema simple con tres subsistemas, o subfunciones, cada una con una confiabilidad estimada de 0.90 (90%) en el momento (t), la confiabilidad del sistema se calcula como 0.90 X 0.90 X 0.90 = 0.729, o aproximadamente 73%.
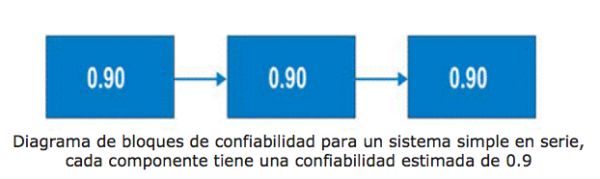
Figura 9. Sistema serial simple
Sistemas paralelos
A menudo, los ingenieros de diseño incorporarán redundancia en máquinas críticas. Los ingenieros de confiabilidad llaman a estos sistemas paralelos. Estos sistemas pueden diseñarse como sistemas paralelos activos o sistemas paralelos en espera. El diagrama de bloques para un sistema paralelo simple de dos componentes se muestra en la Figura 10.
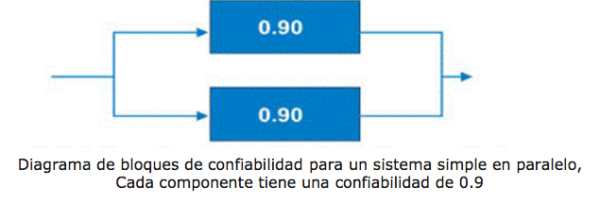
Figura 10. Sistema paralelo simple: la confiabilidad del sistema aumenta al 99% debido a la redundancia.
Para calcular la confiabilidad de un sistema paralelo activo, donde ambas máquinas están funcionando, use la siguiente ecuación simple:
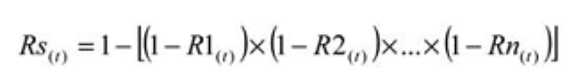
Donde:
Rs (t) – Confiabilidad del sistema para un tiempo dado (t)
R1-n (t) – Confiabilidad del subsistema o subfunción para un tiempo dado (t)
El sistema paralelo simple en nuestro ejemplo con dos componentes en paralelo, cada uno con una confiabilidad de 0.90, tiene una confiabilidad total del sistema de 1 – (0.1 X 0.1) =
0.99. Por lo tanto, la fiabilidad del sistema se mejoró significativamente.
Existen algunos métodos de acceso directo para calcular la confiabilidad del sistema paralelo cuando todos los subsistemas tienen la misma confiabilidad estimada. Más a menudo, los sistemas contienen subcomponentes paralelos y seriales como se muestra en la Figura 11. El cálculo de los sistemas en espera requiere conocimiento sobre la confiabilidad del mecanismo de conmutación. En aras de la simplicidad y la brevedad, este tema se reservará para un artículo futuro.
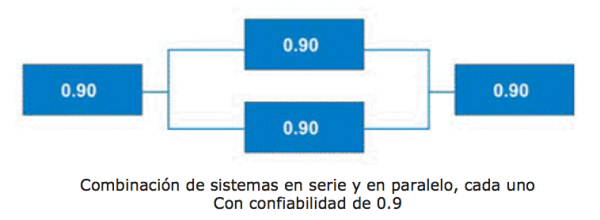
Figura 11. Sistema combinado con elementos paralelos y seriales
Sistemas fuera de n (sistemas r / n)
Un concepto importante para los ingenieros de confiabilidad de planta es el concepto de sistemas r / n. Estos sistemas requieren que r unidades de una población total en n estén disponibles para su uso. Un gran ejemplo industrial son los pulverizadores de carbón en una planta generadora de energía eléctrica. A menudo, los ingenieros diseñan esta función en la planta utilizando un enfoque r / n. Por ejemplo, una unidad tiene cuatro pulverizadores y la unidad requiere que tres de los cuatro funcionen a plena carga de la unidad (ver Figura 12).
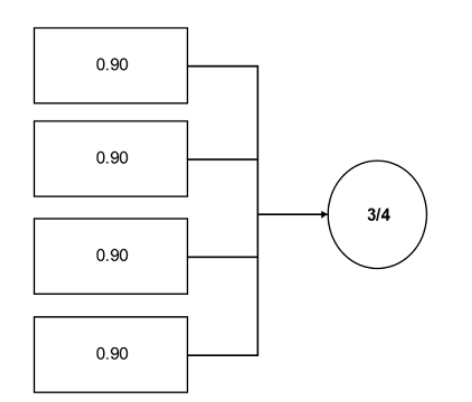
Figura 12. Ejemplo de sistema r / n simple: se requieren tres de los cuatro componentes.
El cálculo de confiabilidad para un sistema r / n se puede reducir a un simple cálculo de distribución binomial acumulativa, cuya fórmula es:
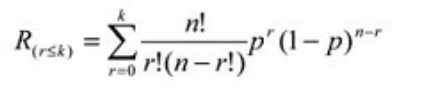
Donde:
Rs = La confiabilidad del sistema dado que el número real de fallas (r) es menor o igual al máximo permitido ( k)
r = El número real de fallas
k = El número máximo permitido de fallas
n = El número total de unidades en el sistema
p = La probabilidad de supervivencia o la confiabilidad del subcomponente para un tiempo dado (t).
Esta ecuación es algo más complicada. Ezn nuestro ejemplo de pulverizador, suponiendo una confiabilidad de subcomponente de 0.90, la ecuación funciona como una suma de lo siguiente:
P (0) = 0.6561
P (1) = 0.2916
Entonces, la probabilidad de completar el tiempo de la misión (t) es 0.9477 (0.6561 + 0.2916), o aproximadamente el 95%.
Recolección de datos de campo
Para emplear los métodos de análisis de confiabilidad descritos en este documento, el ingeniero requiere datos. Es imperativo establecer sistemas de recolección de datos de campo para respaldar sus iniciativas de gestión de confiabilidad. Del mismo modo, tanto como sea posible, querrá emplear nomenclatura y unidades comunes para que sus datos puedan analizarse de manera efectiva para un análisis más detallado. Recopile la siguiente información:
- Información básica del sistema
- Contexto operativo
- Contexto ambiental
- Datos de falla
Un buen sistema general para la recopilación de datos se describe en la norma IEC 300-3-2. Además de proporcionar instrucciones para recopilar datos de campo, proporciona una taxonomía estándar de modos de falla. Se han establecido otras taxonomías, pero el estándar IEC representa un buen punto de partida para que su organización de na el suyo. Del mismo modo, el estándar NE-1004-92 del DOE ofrece una muy buena nomenclatura estándar de causas de falla.
Un beneficio importante derivado de sus esfuerzos por recopilar buenos datos de campo es que le permite romper la “trampa aleatoria”. Como mencioné anteriormente, la curva de la bañera ha sido muy difamada, particularmente en la literatura de Mantenimiento Centrado en Confiabilidad. Si bien es cierto que el análisis de Weibull revela que pocos sistemas mecánicos complejos exhiben fallas de desgaste dependientes del tiempo, la razón, al menos en parte, se debe al hecho de que la confiiabilidad de los sistemas complejos se ve afectada por una amplia variedad de modos y mecanismos de falla.
Cuando estos se agrupan, hay un efecto de “aleatorización”, que hace que las fallas parezcan carecer de dependencia del tiempo. Sin embargo, si los modos de falla fueran analizados individualmente, la historia probablemente sería muy diferente (Figura 13). Por cierto, algunos modos de falla seguirían siendo matemáticamente aleatorios, pero muchos, y posiblemente la mayoría, exhibirían una dependencia del tiempo. Este tipo de información proporcionaría a los ingenieros y gerentes de confiabilidad un poderoso conjunto de opciones para mitigar el riesgo de falla con un alto grado de precisión. Naturalmente, esta capacidad depende de la recopilación efectiva y el posterior análisis de los datos de campo.
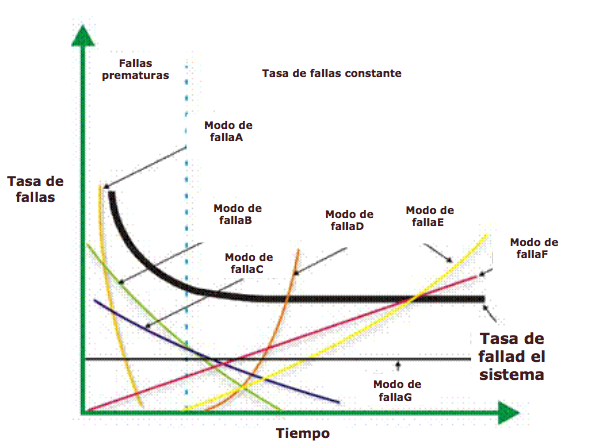
Figura 13. Una buena recopilación de datos de campo le permite romper la trampa aleatoria.
Esta breve introducción a los métodos de ingeniería de confiabilidad está destinada a exponer al ingeniero de planta no iniciado al mundo de la ingeniería de confiabilidad cuantitativa. Sin embargo, el tema es bastante amplio y solo me he referido a los principales métodos de fiabilidad que creo que son más aplicables al ingeniero de planta. Le animo a que investigue más el campo de los métodos de ingeniería de confiabilidad, concentrándose en los siguientes temas, entre otros:
- Comprensión más detallada de la distribución Weibull y sus aplicaciones.
- Comprensión más detallada de la distribución exponencial y sus aplicaciones.
- La distribución gaussiana y sus aplicaciones.
- La distribución log-normal y sus aplicaciones.
- Intervalos de confianza (binomial, chi-cuadrado / Poisson, etc.)
- Distribución beta y sus aplicaciones.
- Aplicaciones bayesianas de métodos de ingeniería de confiabilidad
- Análisis de interferencia de resistencia al estrés
- Opciones de prueba y su aplicabilidad a la ingeniería de confiabilidad de la planta.
- Estrategias y gestión del crecimiento de la fiabilidad.
• Comprensión más detallada de la recopilación de datos de campo.
Lo más importante es pasar tiempo aprendiendo cómo aplicar métodos de ingeniería de confiabilidad a los problemas de confiabilidad de la planta. Si su interés en los métodos de ingeniería de confiabilidad es alto, lo aliento a que busque la certificación profesional de la Sociedad Estadounidense para la Calidad como ingeniero de confiabilidad (CRE).
Referencias
- Troyer, D. (2006) Libro de curso de gestión estratégica de con abilidad de plantas, Noria Publishing, Tulsa, Oklahoma.
- Bernowski, K (1997) “Seguridad en los cielos”, Quality Progress , enero.
- Dovich, R. (1990) Estadísticas de con abilidad, ASQ Quality Press, Milwaukee, WI.
- Krishnamoorthi, KS (1992) Métodos de con abilidad para ingenieros, ASQ Quality Press , Milwaukee, WI. MIL Standard 721
- Norma IEC 300-3-3
- DOE Standard NE-1004-92
Apéndice: Seleccione términos de ingeniería de confiabilidad de MIL STD 721 Disponibilidad: una medida del grado en que un elemento está en el estado operable y comprometible al comienzo de la misión, cuando la misión se solicita en un estado desconocido.
Capacidad: una medida de la capacidad de un elemento para alcanzar los objetivos de la misión dadas las condiciones durante la misión.
Confiabilida: una medida del grado en que un elemento es operable y capaz de realizar su función requerida en cualquier momento (aleatorio) durante un per l de misión específico, dada la disponibilidad al comienzo de la misión.
Falla: el evento, o estado inoperable, en el que un elemento, o parte de un elemento, no funciona o no funcionará como se especificó anteriormente.
Falla, dependiente: falla causada por la falla de uno o varios elementos asociados. No independiente. Falla, independiente: falla que ocurre sin ser causada por la falla de cualquier otro elemento. No dependiente
Mecanismo de falla: el proceso físico, químico, eléctrico, térmico u otro que resulta en una falla.
Modo de falla: la consecuencia del mecanismo a través del cual ocurre la falla, es decir, corto, abierto, fractura, desgaste excesivo.
Falla, aleatoria: falla cuya ocurrencia es predecible solo en el sentido probabilístico o estadístico. Esto se aplica a todas las distribuciones.
Tasa de fallas: la cantidad total de fallas dentro de una población de elementos, dividida por la cantidad total de unidades de vida gastadas por esa población, durante un intervalo de medición particular en las condiciones establecidas.
Mantenibilidad: la medida de la capacidad de un artículo para ser retenido o restaurado a una condición específica cuando el mantenimiento lo realiza personal con niveles de habilidad específicos, utilizando procedimientos y recursos prescritos, en cada nivel prescrito de mantenimiento y reparación.
Mantenimiento, correctivo: todas las acciones realizadas, como resultado de una falla, para restaurar un elemento a una condición especí ca. El mantenimiento correctivo puede incluir cualquiera o todos los siguientes pasos: localización, aislamiento, desmontaje, intercambio, reensamblaje, alineación y verificación.
Mantenimiento preventivo: todas las acciones realizadas en un intento de retener un artículo en una condición específica proporcionando inspección sistemática, detección y prevención de fallas incipientes.
Tiempo medio entre fallas (MTBF): una medida básica de confiabilidad para artículos reparables: el número medio de unidades de vida durante las cuales todas las partes del artículo funcionan dentro de sus límites especificados, durante un intervalo de medición particular en las condiciones establecidas.
Tiempo medio de falla (MTTF): una medida básica de confiabilidad para artículos no reparables: el número medio de unidades de vida durante las cuales todas las partes del artículo funcionan dentro de sus límites especificados, durante un intervalo de medición particular en las condiciones establecidas.
Tiempo medio de reparación (MTTR): una medida básica de mantenimiento: la suma de los tiempos de mantenimiento correctivo en cualquier nivel específico de reparación, dividido por el número total de fallas dentro de un artículo reparado a ese nivel, durante un intervalo particular en las condiciones establecidas.
Fiabilidad de la misión: la capacidad de un elemento para realizar las funciones requeridas durante la duración del per l de misión especificado.
Fiabilidad: (1) La duración o probabilidad de un rendimiento sin fallas en las condiciones establecidas. (2) La probabilidad de que un elemento pueda realizar su función prevista durante un intervalo especificado en las condiciones establecidas. Para elementos no redundantes, esto es equivalente a la definición (1). Para artículos redundantes, esta es la definición de confiabilidad de la misión.
Noria Corporation. Traducido por Roberto Trujillo Corona, Noria Latín América.
 Colombia
Colombia Chile
Chile Costa Rica
Costa Rica Bolivia
Bolivia Perú
Perú Honduras
Honduras El Salvador
El Salvador Guatemala
Guatemala Puerto Rico
Puerto Rico Panama
Panama Paraguay
Paraguay Centro América y Caribe
Centro América y Caribe