Disponibilidad, Confiabilidad, Mantenibilidad y Capacidad son los componentes de la ecuación de efectividad. La ecuación de efectividad es una figura meritoria útil para encontrar cual componente(s) influye(n) negativamente en la medición de desempeño. En muchas plantas con procesos continuos la confiabilidad de un componente es el más grande atacante para un mejor desempeño. En este artículo se ilustra el cálculo de los componentes mediante el uso de pequeños listados de datos.
La Mantenibilidad tiene que ver con la duración de las paradas por Mantenimiento, o en que tanto tiempo se toma en lograr (fácil y rápido) las acciones de mantenimiento, en relación con los
datos. Los datos incluyen el mantenimiento (todas las acciones necesarias para mantener un componente como tal, o restablecerlo a una condición específica) desempeñado por el personal que tiene niveles de especialización, que usa procedimientos y recursos preestablecidos, para cada nivel de mantenimiento establecido. Las características de mantenibilidad son usualmente determinadas por el diseño del equipo, el cual determina los procedimientos de Mantenimiento y la duración de los tiempos de reparación.
El índice clave para la mantenibilidad es frecuentemente el tiempo medio entre reparaciones (MTTR) y es un límite para el tiempo máximo de reparación. Cualitativamente, este se refiere a la facilidad con que el hardware y el software son restablecidos a su estado de funcionamiento. Cuantitativamente este es una probabilidad y es medido con base en el tiempo de parada por mantenimiento, incluyendo todos los tiempos por: diagnóstico, problemas de “descarga”, desarme, remoción/reemplazo, tiempo activo de reparación, pruebas de verificación para saber si la reparación fue adecuada, demoras por movimientos logísticos, y demoras administrativas de mantenimiento. La mantenibilidad es frecuentemente expresada como:
M(t) = 1 – exp(-t/MTTR) = 1 – exp(-μt)
donde μ es la rata constante de Mantenimiento y MTTR es el tiempo medio para reparar. MTTR es
un promedio aritmético de qué tan rápido el sistema es reparado, y se visualiza más fácil que un valor de probabilidad.
Se debe notar que el simple y fácil de usar, criterio mostrado anteriormente, es frecuentemente expresado en tiempos de reparación exponenciales. Una fórmula mejor y más precisa, requiere una ecuación diferente para las complicadas distribuciones log-normal de tiempos de reparaciones, los cuales están distorsionadas hacia la derecha. El resultado de la mantenibilidad es el logro de cortos tiempos de reparación para mantener una alta disponibilidad, de tal manera que sean minimizadas las paradas de los equipos productivos para el control de costos, cuando la disponibilidad es crítica.
Un ejemplo de una meta establecida de mantenibilidad es un 90% de probabilidad de que los tiempos de reparación por Mantenimiento serán completados en 8 horas o menos, con un máximo tiempo de reparación de 24 horas. Esto requiere un MTTR del sistema de 3.48 horas. Además, el tope de 24 horas (99.9% de reparaciones serán completadas en este tiempo, o menos) requiere el control de los tres principales componentes de una parada: 1) el tiempo activo de reparación (una función de diseño, entrenamiento, y especialidad del personal de Mantenimiento), 2) tiempo de logística (tiempo perdido en el suministro de partes de reemplazo), y 3) tiempo administrativo (una función de la estructura operacional de la organización). La probabilidad de no reunir las 8 horas especificadas como intervalo de reparación de este ejemplo, es del 10% basada en un MTTR de 3.48 horas, dado que la mantenibilidad + no-mantenibilidad = 1.
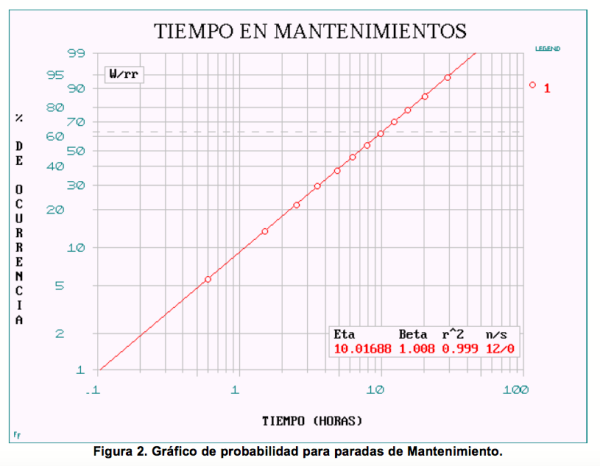
Los datos de la Tabla 1 muestran un tiempo promedio de parada debido a acciones de Mantenimiento de 9.4 horas. El cálculo de la mantenibilidad del sistema usa distribuciones exponenciales mediante las cuales el tiempo de reparación seguido es de 10 horas. El sistema tiene una mantenibilidad de 1 – exp(-10/9.4) = 65.5%. El valor de mantenibilidad es la probabilidad de completar las reparaciones en el intervalo permitido de 10 horas. En pocas palabras, el sistema tiene un valor modesto de mantenibilidad (para el intervalo de reparación permitido de 10 horas)!
Los cálculos anteriores de mantenibilidad fueron obtenidos aritméticamente. Proyecciones más precisas se encuentran construyendo una carta de probabilidad con los datos de la Tabla 1. La Figura 2 muestra el tiempo promedio de paradas para reparaciones de 10 horas. El noventa y ocho por ciento de todos los tiempos de parada por Mantenimiento estarán entre 0.1 horas y 45.6 horas. El diez por ciento de todos los tiempos de parada serán menores de 1.1 horas. El tiempo promedio de parada es de 7.0 horas.
Una nota especial de precaución acerca de la distribución exponencial de la Figura 2. La mayoría de los tiempos de reparación no están distribuidos exponencialmente – usualmente están distribuidos log-normalmente. Sin embargo, no se debe preocuparse mucho por la distribución, dado que el software Weibull WinSMITH permite que muchas diferentes distribuciones sean estudiadas, usando el New Weibull Handbook (Abernethy 1996). Para los ingenieros, el software es muy útil porque los tiempos pueden ser usados para encontrar cosas antes que para especular estadísticamente.
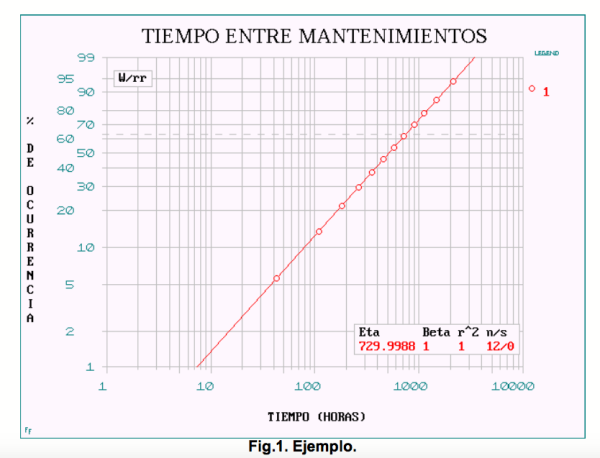
Con los datos de la Figura 1, el MTBM = 730.o horas, y el dato de la Figura 2, MDT = 10.0, puede ser calculada la disponibilidad operacional. Ao = 730/(730 + 10) = 98.6%, el cual es el mismo valor encontrado en el cálculo (tiempo en operación)/(tiempo en operación + tiempo de parada).
Una alta disponibilidad (alto tiempo de operación), alta confiabilidad (pocas fallas) y alta mantenibilidad (tiempos de Mantenimiento cortos y predecibles) son la tendencia de sistemas altamente efectivos si la capacidad es también mantenida en niveles altos.
La Capacidad (N. de T.: en inglés Capability) está relacionada con la entrega productiva comparada con la entrega productiva inherente, la cual es medida en términos de qué tan bien es desempeñada la actividad productiva en comparación con los datos. Este índice mide la capacidad del sistema para desempeñar la función para la cual fue construido sobre la base del sistema. Frecuentemente, este término es sinónimo de productividad, la cual es el producto de la eficiencia multiplicada por la utilización. La eficiencia mide la salida de trabajo productivo versus el trabajo de entrada. La utilización es la relación entre el tiempo gastado en esfuerzos productivos con el total del tiempo consumido.
Por ejemplo, suponga una eficiencia del 80% por pérdidas por material de desecho generado, y una utilización del 82.19% porque la operación es realizada en 300 días por año de 365 días. La capacidad es de 08 * 0.8219 = 65.75%. Estos números son frecuentemente generados por el Departamento de Contabilidad para los Departamentos de Producción como un índice clave de cómo lo están haciendo. Entonces, tales cálculos necesitan pocas explicaciones.
Las Ecuaciones de Efectividad del Sistema (N. de T.: en inglés Efectiveness/LCC) son útiles para entender el benchmarking, pasado, presente, y futuro status, tal como lo muestra la Figura 3, entendiendo la información de «negocio«.
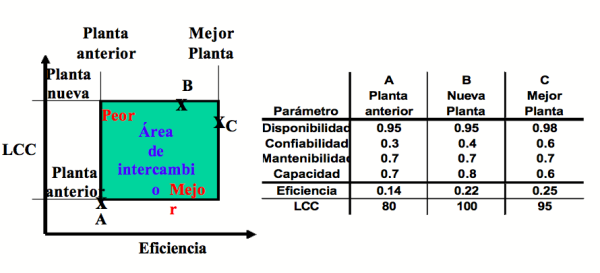
La esquina inferior derecha de la Figura 3 que entrega satisfacción y felicidad, es frecuentemente descrita como “logro del esfuerzo” (Weisz 1996). La esquina superior izquierda genera mucho dolor. Las dos esquinas restantes generan cuestionamientos acerca del trabajo y de los valores.
En Resumen, los elementos de la ecuación de eficiencia suministran una visión acerca de cómo descrita como “logro del esfuerzo” (Weisz 1996). La esquina superior izquierda genera mucho dolor. Las dos esquinas restantes generan cuestionamientos acerca del trabajo y de los valores. las cosas trabajan en un proceso continuo. En la ecuación de eficiencia se dan indicios de donde En Resumen, los elementos de la ecuación de eficiencia suministran una visión acerca de cómo se pueden hacer acciones correctivas, por lo cual es particularmente útil. Esto es importante para las cosas trabajan en un proceso continuo. En la ecuación de eficiencia se dan indicios de donde entender tanto la confiabilidad como la mantenibilidad junto con la información tradicional de se pueden hacer acciones correctivas, por lo cual es particularmente útil. Esto es importante para disponibilidad y capacidad. En todos lo casos, deben ser consideradas varias alternativas, basadas en los costos de ciclos de vida, para priorizar los altos costos de los problemas, de tal manera que los resultados importantes sean identificados para dar las acciones correctivas.
Referencias
- Abernethy, Dr. Robert B. (1996), The New Weibull Handbook, 2nd edición, publicado por el autor.
- Barringer, H. Paul and David Weber (1995), Where is My Data For Making Reliability Improvements? , 4t h conferencia internacional sobre confiabilidad en plantas de procesos, patrocinada por Hydrocarbons Processing and Gulf Publishing Company, Houston, TX.
- Barringer, H. Paul and David Weber (1996), Life Cycle Cost Tutorial, 5th conferencia internacional sobre confiabilidad en plantas de procesos, patrocinada por Hydrocarbons Processing and Gulf Publishing Company, Houston, TX.
- Barringer, H. Paul (1996b), Practical Reliability Tools For Refineries and Chemical Plants, National Petroleum Refiners Association Plant Maintenance Conference and Exhibition, Nashville, TN.
- Barringer, H. Paul (1996c), An Overview Of Reliability Engineering Principles, Energy Week 1996, patrocinado por ASME & API y organizada por Penn Well Conferences, Houston, TX.
- Barringer, H. Paul (1997), Life Cycle Costs & Reliability For Process Equipment, patrocinado por ASME & API y organizada por Penn Well Conferences, Houston, TX.
- Berger, Gene y Herzl Marouni (1993), ASQC Section 1405 Certified Reliability Refresher Course, publicado por Gene Berger, Houston, TX.
- Blanchard, B. S., Dinesh Verma, Elmer L. Peterson 1995, Maintainability: A Key to Effective Serviceability and Maintenance Management, Prentice-Hall, Englewood Cliffs, NJ.
- Clements, Richard Barrett (1991), Handbook of Statistical Methods in Manufacturing, Prentice-Hall, Englewood Cliffs, New Jersey.
- Davidson, John 1988, The Reliability of Mechanical Systems, Mechanical Engineering Publications Limited for The Institution of Mechanical Engineerings, Londres.
- Fulton, Wes (1996), WinSMITH Weibull probability software, versión 1.1P, Fulton Findings.
- Ireson, W. Grant, Clyde F. Coombs, Jr., Richards Y. Moss 1996, Handbook of Reliabilit Engineering and Management, 2nd edición, McGraw-Hill.
- Kececioglu, Dimitri 1995, Maintainability, Availability, & Operational Readiness Engineering, Prentice-Hall PTR, Upper Saddle River, NJ.
- Landers, Richards R. 1996, Product Assurance Dictionary, Marlton Publishers.
- Pecht, Michael 1995, Product Reliability, Maintainability, and Supportability Handbook, CRC Press, Nueva York.
- Raheja, Dev G. 191, Assurance Technologies, McGraw-Hill Inc., Nueva York.
- Weisz, John 1996, “An Integrated Approach to Optimizing System Cost Effectiveness”, 1996 Tutorial Notes Annual Reliability and Maintainability Simposium disponible de Evans Associates, NC.
INFORMACIÓN BIOGRÁFICA
H. Paul Barringer
Consultor sobre fabricación, ingeniería y confiabilidad, y autor del curso de entrenamiento básico en confiabilidad Reliability Engineering Principles. Tiene más de treinta y cinco años de experiencia en fabricación e ingeniería en diseño, producción, calidad, mantenimiento, y confiabilidad de productos técnicos. Contribuyó al The New Weibull Handbook, un texto de ingeniería de confiabilidad publicado por el Dr., Robert B. Abernethy. Nombrado como inventor en seis patentes en los E.E.U.U. Tiene registro profesional de ingeniero en Texas. Su educación incluye un MS y un BS en Ingeniería Mecánica de la North Carolina State University, y ha participado en tres semanas en la conferencia de estrategias de fabricación de la Universidad de Harvard.
Noria Corporation. Traducido por Roberto Trujillo Corona, Noria Latín América.














