Utilice el Análisis Estadístico para Crear Límites para Partículas de Desgaste

Una de las preguntas más frecuentes realizadas a los laboratorios de análisis de aceite es “¿Cuál es el límite critico en metales de desgaste para mi equipo? Por años, los laboratorios de análisis de aceite han sido reacios a suministrar ese tipo de información. Esto se debe particularmente a que no todos los laboratorios han establecido correctamente los límites de desgaste, y suministrando esta información a supervisores de mantenimiento poco entrenados puede resultar en reparaciones prematuras e injustificadas. Con un enfoque actual de mantenimiento más sofisticado e ingenieros y supervisores más preparados, es más fácil explicar y justificar límites condenatorios para una gran variedad de componentes de máquinas.

Esto permite a los usuarios del análisis de aceite tomar el control de la interpretación y administración de los resultados. Este artículo está enfocado hacia el establecimiento de límites en partículas de desgaste comúnmente utilizado por laboratorios comerciales de análisis de aceite y los fabricantes de equipos – uno que pueda ser adaptado fácilmente para permitir a los usuarios de análisis de aceite establecer sus propios límites en partículas de desgaste.

Límites Estadísticos de Metales de Desgaste

El uso de la estadística es esencial para establecer límites en cuanto a la concentración de metales de desgaste. Los laboratorios de análisis de aceite y los fabricantes de equipos utilizan algunos métodos para determinar los límites de metales de desgaste. La más común, y que se adapta más rápidamente para que los usuarios definan sus límites, es el uso de un modelo simple estadísticos para analizar el universo de resultados procedentes de componentes similares. Este modelo asume que la concentración de elementos de equipos similares cae dentro de una distribución normal (Figura 1). En una distribución normal, el promedio (x) de todos los datos es el valor reportado más común, con una cierta probabilidad, como se indica, de que las lecturas pueden caer por encima o por debajo de este valor.

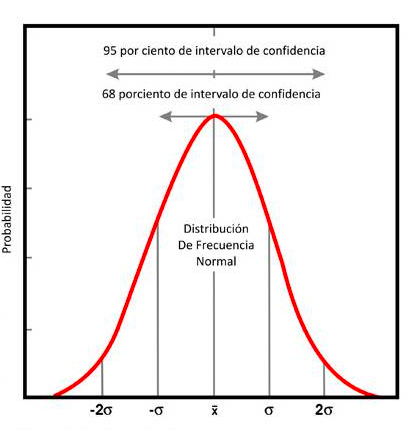
Figura 1. Curva de Frecuencia

Para calcular el promedio, sume todos los datos y divídalos por el número de datos.

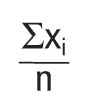
Sin embargo, lo que se requiere para definir lo que es normal bajo este tipo de distribución es conocer no solamente el promedio de todos los datos, sino también el rango de valores que es posible, representado por el ancho de la curva (Figura 1). Para definir el ancho o rango, los estadísticos introducen el concepto de desviación estándar, la cual en términos generales es una medida del ancho o rango de una distribución normal. La desviación estándar, representada por la letra griega σ, puede ser calculada utilizando la siguiente fórmula matemática:

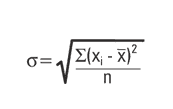
En esta ecuación, xi representa cada resultado o dato, ẋ es el promedio de todos los datos, y ƞ el número total de datos. La Tabla 1 muestra un ejemplo de cómo se puede calcular σbasado en los datos de 10 resultados simples.

Suponiendo una distribución normal, cualquier lectura que caiga entre x ± σ está en dentro del 68 por ciento de todos los valores; los limites de precaución para el análisis de metales de desgaste que utilizan este enfoque se establecen en x ± σ. Expandiendo el intervalo a x ± 2σ significa que cualquier lectura que caiga dentro de este rango está dentro del 95 por ciento de todos los valores. x ± 2σ es normalmente utilizado como el límite condenatorio para concentraciones de metales de desgaste. Basado en esto y en los resultados dados en la Tabla 1, el límite de precaución para estos resultados debería ser de 28.0 (x ± σ), y el límite crítico en 33.3 (x ± 2σ).

El valor de esta forma de establecer los límites de desgaste es que este representa con bastante exactitud la concentración esperada de metales de desgaste en las muestras de aceite usado – siempre que el conjunto de datos se seleccione de manera adecuada y que sea lo suficientemente grande (normalmente > 25 datos se considera suficiente). La mayoría de los programas comerciales de análisis de aceite, al igual que las conocidas hojas de cálculo, son capaces de calcular directamente el promedio y la desviación estándar de un grupo seleccionado de muestras, simplificándole la tarea de la definición de límites al usuario.

Selección de Resultados

La precisión de la distribución normal para establecer las alarmas para los metales de desgaste depende no solamente del tamaño de la base de datos, sino también de la similitud de los componentes y los resultados de las muestras de donde se seleccionan los datos. Por ejemplo, tomar simplemente los datos de desgaste de todos los componentes identificados como caja de engranajes no suministra una descripción detallada para obtener resultados precisos. Esto se debe a que las tasas de desgaste de cada caja de engranajes depende del tipo de engranaje (hipoidal, recto, etc.), la metalurgia (acero al carbono, bronce fundido, etc.), la aplicación y carga a la cual el engranaje está sometido y muchos otros factores. El criterio de selección que debería ser utilizado para definir los componentes que deben ser incluidos en una base de datos se muestran en la Pirámide (Figura 2).

Es importante notar que con cada cambio en los criterios de selección, los resultados de las muestras a usar en la base de datos cambian significativamente, dando como resultados alarmas y límites diferentes. Por ejemplo, una transmisión. Usando la descripción transmisión de cambios auto/asistida puede llevarnos a los limites condenatorios descritos en la Figura 3a basados en los resultados de las muestras seleccionadas bajo el termino general de transmisión. Añadiendo una descripción más específica, en este caso el fabricante Allison, para redefinir la base de datos, da como resultado un cambio significativo en el cálculo de los limites de alarma Figura 3b. Si además redefinimos la base de datos agregando el modelo de la transmisión, esto da como resultado otro cambio significativo en los límites de alarma Figura 3c. En general, mientras se utilicen más detalles para definir la base de datos, más precisos serán el análisis estadístico y el establecimiento de los límites. De hecho, redefiniendo la base de datos de acuerdo con los criterios indicados en la Figura 2, los datos pueden ser redefinidos de tal manera que el análisis estadístico sería verdaderamente representativo de lo que se consideraría normal para un componente específico y además de alarmas y limites más precisos y significativos.

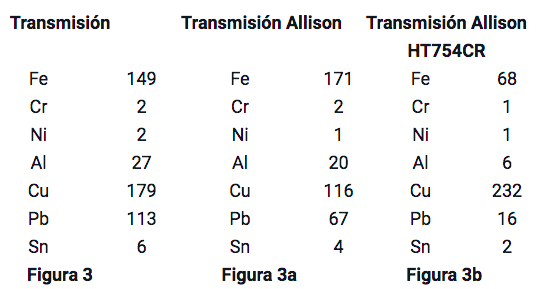
Figura 2.

Noria Corporation. Traducido por Roberto Trujillo Corona, Noria Latín América.