El análisis de Weibull es la técnica mayormente elegida para estimar una probabilidad, basada en datos medidos o asumidos. La distribución de Weibull descubierta por el sueco Walodi Weibull, fue anunciada por primera vez en un escrito en 1951. La distribución de Weibull es útil por su habilidad para simular un amplio rango de distribuciones como la Normal, la Exponencial, etc. Las técnicas discutidas en la distribución de Weibull son similares a las usadas con las distribuciones Normal y Log-Normal. Este artículo le dará una visión general de la aplicación de la distribución de Weibull.
Permítame nombrarlo a usted como miembro principal del Comité de Refrigerios de un equipo de béisbol. Suponga que usted compra 800 perros calientes (“hot dogs”) cada semana, y toma nota del número de perros calientes que realmente vende en un partido de béisbol universitario. En los primeros siete juegos las cifras son:
492 287 521 604 349 453 412
El presidente de su Comité de Refrigerios quiere reducir los costos para mantener contentos a los propietarios. El presidente quiere que usted compre solamente los suficientes perros calientes la próxima vez, de tal manera que solo en el 15% de las veces no hayan suficientes perros calientes (en el 85% de las veces habrán suficientes perros calientes para vender). Usted consulta a su profesor de estadística quien le indica acerca de utilizar el ANÁLISIS DE WEIBULL, dado que la cantidad de perros calientes vendida es aproximadamente un número aleatoriamente variable.
Su profesor de estadística, con ayuda de un software o simplemente a mano, tabula los siete datos iniciales y procede a calcular lo que se conoce como RANGO MEDIO, para cada uno de ellos. El Rango Medio es un número entre 0 a 1 que refleja en orden ascendente la fracción del valor del dato que es menor que el mismo dato. Así, se obtiene la Tabla 1, una vez ordenados los datos.
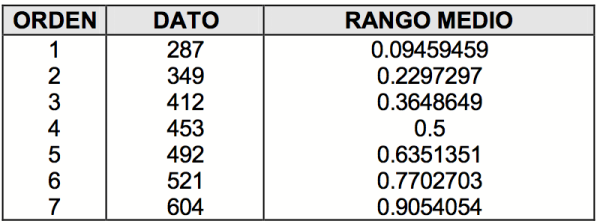
Tabla 1.
En la tabla 1, hay un 90.5% de posibilidades que el número de perros calientes vendidos sea menor a 604, dado que el Rango Medio para este último punto es de 0.9054054. Usualmente, el Rango Medio se puede encontrar en los libros de estadística, o puede ser calculado con la fórmula de Bernard.
Si se dibuja en un gráfico el doble logaritmo de 1/(1 – Rango Medio) vs. el logaritmo de los datos en cuestión, se obtiene el Gráfico de Weibull (ver Fig. 1). Usualmente, la mayoría de los datos a analizar forman una línea recta en esta gráfica. Esta línea recta puede ser trazada por el método de la regresión o de los mínimos cuadrados.
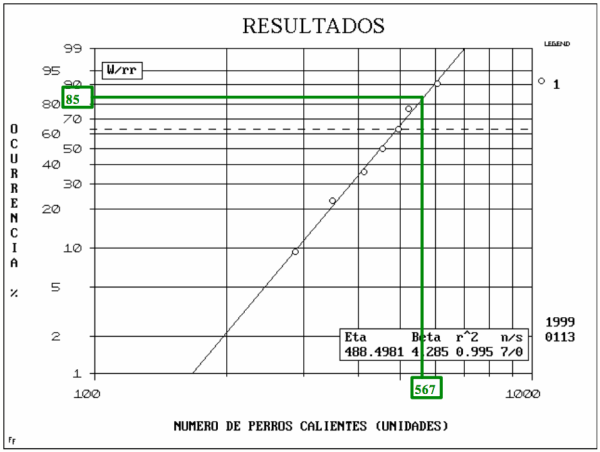
Fig. 1. Gráfico de Weibull
La ecuación de la distribución acumulativa de Weibull es:
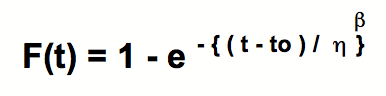
donde:

La pendiente de la línea recta que pasa por la mayoría de los puntos en el Gráfico de Weibull, es también el Factor de Forma β. Esta β indica el tipo de distribución de probabilidad (normal, exponencial, etc.).
La Vida Característica η es el valor del dato (en este caso: número de perros calientes) que corresponde al 63.2% del valor del Rango Medio de la línea recta. Este 63.2% es realmente 1 – 1/e, dado to = 0 y t = η. En el Gráfico de Weibull, usted puede hacer estimaciones de probabilidades utilizando la línea recta, o simplemente leyendo la probabilidad en la escala vertical, para un dato (en este caso, un número de perros calientes).
Volviendo al ejemplo, el número estimado de perros calientes a comprar, para un 15% de veces no satisfechas, se localiza en la línea recta con una probabilidad de 0.85 (85%). Para este dato, el punto ocurre a los 567 perros calientes. Problema resuelto.
Pero, espere un momento. ¿Cómo asegura usted este tipo de análisis?
La respuesta es …… aproximadamente en un 50% (según la estadística). Esto es, con 567 perros calientes en el próximo juego de béisbol usted tiene un 15% de probabilidad de que tenga menos perros calientes de los requeridos, o que tenga un 15% más de los perros vendidos (el Rango Medio implica un 50 – 50 de posibilidades para la probabilidad real, siendo más bajo a más alto de lo estimado). Dado que su presidente de comité le dice que usted deberá asegurarse en un 90% de que los clientes no atendidos sean menores al 15%, usted deberá tener CONFIABILIDAD (algunos autores la llaman Confianza).
Usted puede obtener la confiabilidad requerida para valores diferentes al 50% (Rango Medio). Para el efecto, debe trazar sobre el mismo Gráfico de Weibull la línea de confiabilidad superior del 90%, la cual usualmente es curva (Ver Fig. 2).
En la Fig. 2, entrando por la escala vertical con un 85% de ocurrencia hasta la línea curva de confiabilidad del 90%, y bajando verticalmente, se encuentra en la escala horizontal con un valor de 647 perros calientes. Esa es la cantidad (647) que usted deberá comprar para el próximo partido, para que por lo menos tenga un 85% de posibilidades de satisfacer a todos los futuros clientes con un 90 de confianza (Confiabilidad).
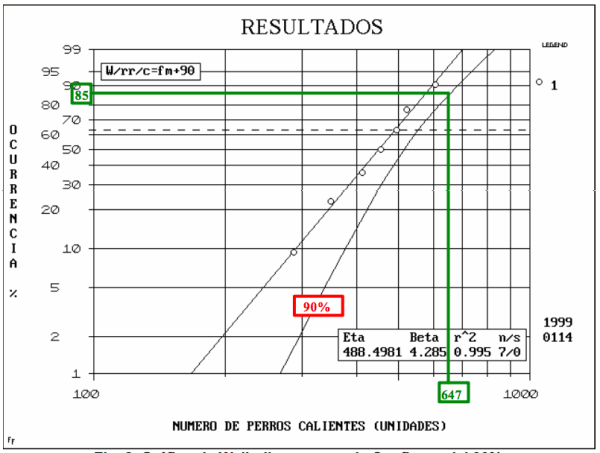
Fig. 2. Gráfico de Weibull con curva de Confianza del 90%
Pero, otro momento. Suponga ahora que en un nuevo partido (octavo) a la altura del séptimo inning empezó a llover fuertemente, se suspendió el partido y usted solamente había vendido 370 perros calientes. Usted sabe que habría podido vender más (mas de 370 perros calientes) si no hubiera llovido. Este dato, por su característica, se llama SUSPENDIDO y debe tenerse en cuenta para el cálculo total, por lo que la mayoría de software lo considera y le da un tratamiento especial (por convención: -370), el cual afecta los rangos medios (Ver Tabla 2).
El tercer punto en la Tabla 2 es el valor de dato de suspensión (-370). Usualmente, los números de secuencia después de una suspensión no son enteros.
Continuando con el ejemplo, el número de perros calientes que usted debe comprar, para tener un 85% de posibilidades de satisfacer a todos sus clientes, con un 90% de confianza (Confiabilidad) es de 641, debido a la adición de este nuevo dato de suspensión (Ver Fig. 3).
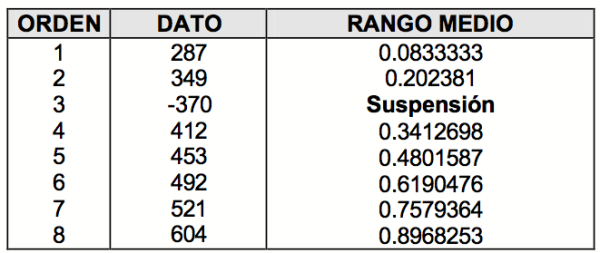
Tabla 2
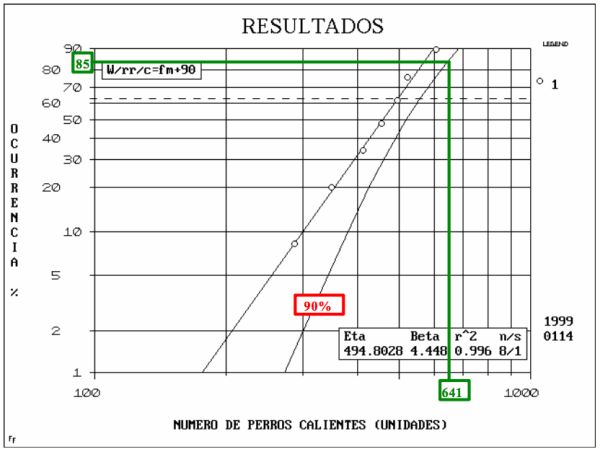
Fig. 3. Gráfico de Weibull con curva de Confianza del 90% y 1 Suspensión
Con esta información, usted regresa a donde su presidente de comité, le muestra los resultados y le indica el ahorro de 800 – 641 = 159 perros calientes por partido. Felicitaciones, ha concluido usted con éxito su análisis, con un ahorro considerable para su Comité.
OTROS CASOS
La técnica de Weibull puede ser usada para estimar la probabilidad en numerosos casos. Es frecuente emplearla en estimar la vida de los rodamientos. La vida B-10 (falla del 10%) se obtiene cuando se prueban rodamientos nuevos bajo condiciones de carga, velocidad y lubricación específicas, con un resultado de falla del 10% de los rodamientos.
Suponga que usted ha probado 4 rodamientos y registrado la vida útil de cada uno de ellos: 55, 70, 40, y 65 horas. Usted puede obtener la vida B-10 graficando los datos mediante la técnica de Weibull. La vida B-10 se obtiene localizando el 10% en la línea de ocurrencia sobre el eje vertical y encontrando el punto en el eje horizontal correspondiente. Así, para el ejemplo, la vida B-10 es de 34 horas (Ver Fig. 4). Esto quiere decir, que a las 34 horas de operación, y para esos rodamientos en particular, fallarán un 10% de ellos.
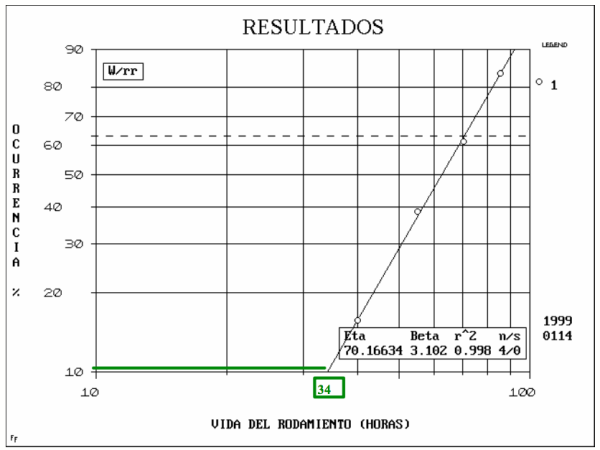
Fig. 4. Gráfico de Weibull para el ejemplo de los rodamientos
Traducido y adaptado por Héctor Danilo Ordóñez Lozano














